Nasz tytułowy bohater jest słynnym podróżnikiem, pochodzącym z Programinii. W kraju tym, wszyscy w zależności od regionu czy miasta mówią różnymi językami programowania. Na przykład w Trójmieście Języków C, gdzie miasta to: City, City++ i City#, ludzie mówią odpowiednio w języku C, C++ i C#. Ciekawym regionem jest również Okręg Przemysłowy Brainf*cktory, gdzie mówi się, a jakże, w Brainf*cku. Wróćmy, więc do naszego podróżnika. Król Asemblord – władca Programinii, zlecił mu misję zbadania odległych krain, leżących poza Programinią. Tym razem Informatyk Jones udał się do bardzo dziwnego kraju. Istoty tam żyjące nie mówią językiem programowania, lecz normalnym językiem z gramatyką. Długo zajęło mu poznanie i nauczenie się owej mowy, lecz w końcu udało się i zapragnął stopniowo wysyłać królowi tajniki jej gramatyki, lecz biorąc pod uwagę charakterystykę Programinii, nie pisał on zwykłych listów, lecz programy. Wysyłając „list” opisujący zasady tworzenia liczby mnogiej, napotkał pewne problemy. Oto zasady jej tworzenia:

- jeżeli w wyrazie występuje samogłoska –e to –e zmienia się w –i oraz jeżeli w wyrazie występuje samogłoska –a to –a zmienia się w –e,

- jeżeli w wyrazie nie występują samogłoski –a ani –e, ale jeżeli występuje samogłoska –o to –o zmienia się w –e, jeżeli –o, ani –a, ani –e nie występuje, ale występuje –u to –u zamieniamy w –e i jeżeli żadna z wymienionych samogłosek nie występuje to, jeżeli występuje samogłoska –y to –y zmienia się w –e,

- samogłoska –i nie ulega żadnym zmianom.

Zasady wydają się proste, lecz język ten charakteryzuje się pewnymi nadrzędnymi regułami:

- w każdym wyrazie musi znajdować się co najmniej jedna samogłoska,

- dwie lub więcej takich samych samogłosek nie mogą występować obok siebie, czyli połączenia typu –aa, -ee, –oo, -uu, -ii -yy są niedozwolone,

- samogłoski nie mogą być używane jako półsamogłoski, czyli –i nie może być używane jako –j, oznacza to, że nie mogą występować takie połączenia jak –ie, -ia, -io, iu, iy, chyba, że przed takim połączeniem występuje spółgłoska –n, wtedy należy to przeczytać jako polskie –ń oraz połączenie może być dozwolone, jeżeli przed połączeniem –ie występuje –k lub –g, ponieważ wtedy czytamy tak jak po polsku np. w wyrazach kiełbasa czy kiełki (połączenia –ei, -ai, –oi -ui, yi są jak najbardziej dozwolone).

Wciel się w rolę słynnego podróżnika Informatyka Jonesa i prześlij królowi „list”, w którym zostaną omówione zasady tworzenia liczby mnogiej. Nie trzeba się obawiać, że król nie zrozumie „listu”, ponieważ zna on wszystkie języki programowania. Zważ każde słowo, ponieważ władca Programinii posiada osobistego cenzora SPOJusza, który przedstawia królowi tylko poprawnie napisane „listy”. 

Wejście

W pierwszym wierszu zostanie podana jedna, niewielka liczba naturalna t określająca liczę zestawów danych. Każdy zestaw składa się z jednego wyrazu zawierającego maksymalnie 25 znaków, będących jedynie małymi literami alfabetu łacińskiego (wszystkimi oprócz x i v) (wyrazy mogą, ale nie muszą spełniać zasad tego języka).

Wyjście

Na wyjściu należy podać liczbę mnogą, utworzoną od danego wyrazu (zgodnie z zasadami omówionymi powyżej). Samogłoski -a oraz -e należy zamieniać jednocześnie. Jeżeli w wyrazie pewna samogłoska nie może zostać zamieniona, ponieważ zamiana ta spowodowałaby złamanie którejkolwiek z reguł nadrzędnych, to nie zamieniamy danej samogłoski. Jeżeli w wyrazie pewna samogłoska nie może zostać zamieniona to nie oznacza to, że inne także nie mogą zostać zamienione. Jeżeli wyraz na wejściu nie spełnia którejkolwiek z reguł nadrzędnych należy wypisać: „wyraz niezgodny z zasadami mowy”. 

Przykład

Wejście:

13
bool
sqrt
io
hila
gaur
huo
onge
niea
feal
esa
kear
seanta
eao
Wyjście:

wyraz niezgodny z zasadami mowy
wyraz niezgodny z zasadami mowy
wyraz niezgodny z zasadami mowy
hile
geur
hue
ongi
niea
feal
ise
kier
seante
eao

Zapewne każdy z nas słyszał o sandboxowej grze, jaką jest Minecraft(coś wspaniałego ). Jako że zawsze bardzo interesowała mnie informatyka, najbardziej lubiłem tworzyć różnego rodzaju mechanizmy, bramki logiczne itp. Czerwony proszek — tzw. redstone był jednym z kluczowych dla mnie elementów rozgrywki, który służył do zasilania maszyn, bramek logicznych, ... Zmodyfikujmy trochę zasady gry i przenieśmy tę analogię — napiszmy program, który sprawdzi, czy jesteśmy w stanie przeprowadzić energię przez obszar o wymiarach 10 na 10. Zaczynamy w punkcie (0,0), wprowadzając tu energię na redstone, która musi dotrzeć do punktu (9,9), również na redstone. Wyjaśnijmy zasady. Energia może poruszać się tylko w poziomie i pionie, po czerwonym proszku (oznaczamy 'R'). Energia może przemieszczać się w zasięgu maksymalnie pięciu jednostek, długością tzw. sznura. Jeśli po pięciu jednostkach nie napotka wzmacniacza, tzw. repeatera (oznaczamy 'P'), to nie będzie w stanie pójść dalej. Jeśli zaś napotka wzmacniacz po pięciu jednostkach lub wcześniej, będzie w stanie przemieścić się kolejne pięć jednostek, w każdą następną stronę. Energia nie jest w stanie przenosić się bezpośrednio ze wzmacniacza na wzmacniacz. Drogi nie łączą się oraz nie zapętlają, również nie do chodzi do sytuacji, w której czerwony proszek przebiega bezpośrednio obok drugiego, łącząc się z nim, tworząc tzw. sieci(pola). Całą resztę oznaczamy dowolnymi innymi znakami np. 'O'.

Wejście

Na wejście programu zostanie podana pewna nieokreślona ilość 100-znakowych łańcuchów znaków, reprezentujących zawartość obszaru. Każdy łańcuch oddzielony jest znakiem nowej linii.

Wyjście

Na wyjściu programu ma pojawić się ciąg binarny, odpowiadający wejściu. Jeśli jesteśmy w stanie przeprowadzić energię z punktu (0,0) do punktu (9,9), wypisujemy 1, jeśli nie, to 0.

Przykład

Wejście:
RROOOOOOOOORROOOOOOOOORPOOOOOOOOORROOOOOOOOORROOOOOOOOORPOOOOOOOOORROOOOOOOOORROOOOOOOOORPOOOOOOOOOR
ROOOOOOOOOROOOOOOOOOROOOOOOOOOROOOOOOOOOROOOOOOOOOPOOOOOOOOOROOOOOOOOOROOOOOOOOOROOOOOOOOORRPRRRRRRR

Wyjście:
1 
0

FR_07_09 - System liczbowy inny niż inne

 

Na temat systemów liczbowych można pisać bardzo wiele. Ulubionym system dla ludzi jest system dziesiętny. Wszelkie wartości liczb zapisane za pomocą dziesięciu cyfr są doskonale rozumiane i raczej nie wyobrażamy sobie aby używać innego. Komputery lubują się w systemie dwójkowym, a w Trójkolandii obowiązującym systemem jest system trójkowy. Zaważ, że w każdym wspomnianym systemie podstawa jest stała - w dziesiętnym jest to liczba 10, natomiast w dwójkowym liczba 2. W tym zadaniu zajmiemy się systemem, w którym mnożniki kolejnych pozycji nie są zdefiniowane w postaci potęgi pewnej podstawy tylko przez silnię kolejnych liczb naturalnych dodatnich.

Np. liczba

(100)₁₀ = 4⋅4! + 0⋅3! + 2⋅2! + 0⋅1! = (4020)_!

 Zadanie polega na zamianie liczby z systemy dziesiętnego na opisany w treści zadania. Rozpatrujemy cyfry: {0, 1, 3, ..,9, A, B, ...}. 

Wejście

W pierwszym wierszu jedna liczba t określająca liczbę zestawów danych (nie więcej niż 10⁶).

W kolejnych t wierszach po jednej liczbie całkowitej a zapisanej w systemie dziesiętnym mieszczącej się w przedziale [0..2⁶⁴-1].

Wyjście

Dla każdego zestawu testowego po jednej liczbie zapisanej w systemie silniowym.

Przykład

Wejście:
3
10
100
0

Wyjście:
120
4020
0

FR_07_10 - Szyfr vs kwadraty

 

Znany kryptograf i doradca prezydencki profesor Algobit opracował kwadratowy system szyfrujący, który będzie chronił wszystkie strategiczne informacje Państwa. Prace nad tym skomplikowanym szyfrem trwały miesiącami. Kryptoanalizą zajmowały się najlepsze specjalistki w tej dziedzinie. Stwierdzono jednoznacznie, że utworzony system jest bezpieczny i bez znajomości podstaw działania systemu nie da się go złamać. Jeśli jednak nie zgadzasz się z tym co tu napisałem, spróbuj obalić tą teorię i odszyfruj szyfrogram dowodząc swojej ogromnej inteligencji :).

Wejście

Pewna nieokreślona liczba wierszy. W każdym wierszu jedno zadanie do odszyfrowania. Liczba znaków jest nie większa niz 1024.

Wyjście

Dla każdego wiersza oryginalna wiadomość.

Przykład

Wejście:
AMO LAT A A  K  
BKLKO O LIL E E 
FKLRT AA 

Wyjścia nie podano celowo.

FR_07_11 - Mieszanie tablicy

 

Przydatną funkcją jest system mieszający elementy tablicy. Poniżej znajduje się opis takiego systemu:

Zasada mieszania:

Wyobraźmy sobie trzy struktury działające w następujący sposób:

1. Struktura pierwsza (stos): element, który jako ostatni został dodany, jako pierwszy będzie zdjęty i usunięty ze struktury, itd..
2. Struktura druga (kolejka FIFO): element, który jako pierwszy został dodany, jako pierwszy będzie zdjęty i usunięty ze struktury, itd.
3. Struktura trzecia (kolejka priorytetowa): element, który ma największą wartość, będzie zdjęty jako pierwszy i usunięty ze struktury, itd.

Elementy tablicy, które chcemy wymieszać dodajemy cyklicznie do struktury nr 1, 2 oraz 3. Następnie w ten sam sposób zdejmujemy ze struktur. 

Na wejściu pojawią się elementy tablicy już pomieszane, twoim zadaniem jest wypisanie kolejnych elementów tablicy w pierwotnym ich ustawieniu. Uwaga! Jeśli istnieje kilka prawidłowych odpowiedzi, wypisujemy dowolną.

Wejście

W pierwszym wierszu jedna liczba n określająca liczbę elementów tablicy (nie więcej niż 2 000 000). 

W drugim wierszu n liczb całkowitych. Każda z nich mieści się w przedziale [-10⁹..10⁹].

Wyjście

Na wyjściu wypisujemy przykładowe pierwotne ustawienie elementów tablicy.

Przykład

Wejście:
10
10 2 9 7 5 6 4 8 3 1 

Wyjście:
1 2 3 4 5 6 7 8 9 10 

FR_07_12 - Czerwone mrówki

 

Czerwone mrówki

Przyrodnik Jasiu postanowił zbadać wścieklice, mrówki popularnie nazywane czerwonymi. W tym celu udał się do pobliskiego lasu, aby je poobserwować. Zdziwił się trochę, gdy zauważył, że kolonia czerwonych mrówek wymieszała się z kolonią rudnic. Postanowił zrobić trochę zdjęć. Po powrocie do domu zabrał się do analizowania zrobionych przez siebie zdjęć. Naszego przyrodnika interesuje, jaka jest liczebność wszystkich mrówek w najmniejszym prostokątnym obszarze, do którego należą wszystkie mrówki czerwone. Boki takiego prostokątnego obszaru muszą być równoległe do osi układu współrzędnych. Każda mrówka na zdjęciu opisana została za pomocą współrzędnych kartezjańskich oraz wartości 1 albo 0, gdzie 1 oznacza mrówkę czerwoną, a 0 oznacza mrówkę czarną. Teraz wystarczy już tylko napisać program, aby zaoszczędzić naszemu przyrodnikowi trochę czasu. 

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę zestawów danych - zdjęć. W pierwszym wierszu każdego zestawu znajduje się liczba całkowita n (2 ≤ n ≤ 10⁵) oznaczająca liczebność mrówek na zdjęciu. W kolejnych n wierszach podane są po trzy liczby całkowite x, y, k (0 ≤ x, y ≤ 10³, k={0,1}), gdzie wartości x, y oznaczają współrzędne kartezjańskie mrówki, a k to jej kolor. Dla k = 1 mrówka jest czerwona, dla k = 0 mrówka jest czarna. Można założyć, że żadna mrówka nie łazi po innej mrówce oraz, że rozmiar plików wejściowych nie przekracza 4 MB. 

Wyjście
Dla każdego zestawu należy wypisać w osobnym wierszu jedną liczbę - liczebność wszystkich mrówek zawierających się w najmniejszym prostokątnym obszarze, do którego należą wszystkie mrówki czerwone.


Przykład

Wejście
1
9
6 3 1
1 2 0
7 2 0
5 1 1
2 5 0
4 4 0
1 4 1
3 3 0
5 7 0

Wyjście
6

Rysunek do przykładu
Mrówki czerwone jak i brzeg prostokątnego obszaru został oznaczony kolorem czerwonym. W prostokącie tym znajduje się łącznie sześć mrówek.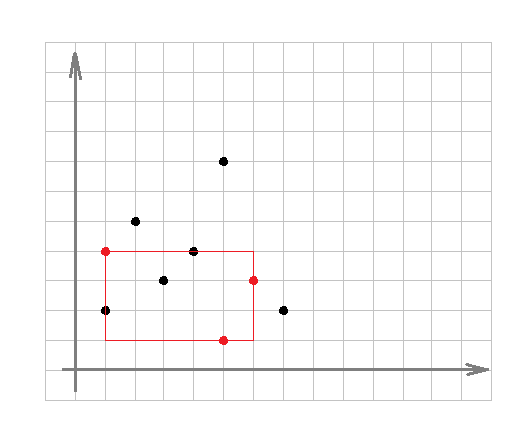

FR_07_13 - Strzelec wyborowy

 

Należy określić, czy pozycja strzelca pozwoli trawić w cel. Rozpatrujemy sytuację, gdzie podany jest punkt kartezjański, oznaczający pozycję strzelca, odcinek równoległy do osi OY będący celem oraz odcinek także równoległy do osi OY będący przeszkodą. Należy sprawdzić, czy przeszkoda nie zasłania całkowicie celu, tzn. czy strzelec jest w stanie trafić w dowolny punkt z przedziału obustronnie otwartego (y_c1, y_c2).

Wejście

W pierwszym wierszu trzy liczby całkowite: y_c1, y_c2, x_c określające współrzędne celu będącego odcinkiem połączonym punktami o współrzędnych (x_c, y_c1) i (x_c, y_c2), (-10⁶< y_c1 < y_c2 < 10⁶, |x_c| < 10⁶).

W drugim jedna liczba q określająca liczbę zapytań (conajmniej jedno i nie więcej niż 1000).

Specyfikacja każdego zapytania:

W pierwszym wierszu współrzędne przeszkody, w drugim współrzędne strzelca.

Przeszkoda określona jest w postaci trzech liczb całkowitych y_p1, y_p2 oraz x_p, określającymi przeszkodę będącą odcinkiem połączonym punktami o współrzędnych (x_p, y_p1) i (x_p, y_p2), (-10⁶< y_p1 < y_p2 < 10⁶, |x_p| < 10⁶).

Współrzędne strzelca to dwie liczby całkowite x i y, gdzie x > x_c oraz |y| < 10⁶. Odcinki ani pozycja celu nie nachodzą na siebie. 

Wyjście

Dla każdego zapytania napis TAK jeśli strzelec ma możliwość trafienia do celu lub NIE, gdy takiej możliwości brak.

Przykład

Wejście:
1 3 -4
2
-1 1 1
3 -1
2 3 2
4 2

Wyjście:
NIE
TAK

Ilustracja przykładu

 

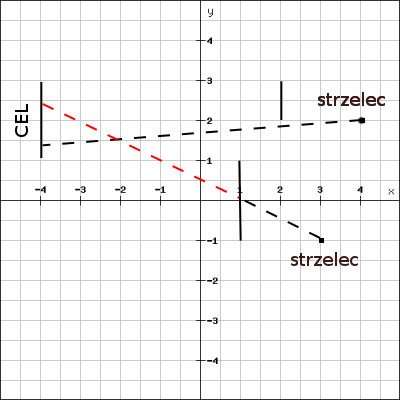
FR_07_14 - Plaster miodu

 

Plaster miodu

Narysuj plaster miodu złożony z n kolumn, po mkomórek w każdej kolumnie.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę przypadków testowych. Każdy zestaw składa się z dwóch wierszy. W pierwszym wierszu podana jest liczba całkowita k (1 ≤ k≤ 100) oznaczająca liczbę kolumn plastra miodu. W wierszu drugim podanych jest k liczb całkowitych m (1 ≤ m ≤ 100) oznaczających liczebność sześciokątnych komórek w kolejnych kolumnach plastra miodu. 

Wyjście
Dla każdego przypadku testowego należy narysować właściwy plaster miodu używając trzech znaków: _, /, \, znaku spacji i znaku końca linii tak, jak to pokazane jest w przykładowym wyjściu. Każdy rysunek kończy znak końca linii.

Przykład

Wejście
2
4
1 1 1 1
5
3 4 1 2 4

Wyjście
 _   _   
/ \_/ \_ 
\_/ \_/ \
  \_/ \_/
 _   _   _ 
/ \_/ \_/ \
\_/ \_/ \_/
/ \_/ \_/ \
\_/ \ / \_/
/ \_/ \_/ \
\_/ \   \_/
  \_/   / \
  / \   \_/
  \_/      

FR_07_15 - Sfeniczne i nie tylko

 

Miałeś już okazję zapoznać się z liczbami sfenicznymi chociażby rozwiązując jedno z zadań próbnym VII edycji konkursu "FRAKTAL". Przypomnijmy: liczba sfeniczna, to taka liczba naturalna, która rozkłada się na iloczyn dokładnie trzech różnych liczb pierwszych. Utrudnijmy to zadanie i zdefiniujmy liczbę k-sfeniczną. Liczbę k-sfeniczną nazywamy taką, która rozłoży się na iloczyn dokładnie k różnych liczb pierwszych. Zadanie polega na napisaniu programu, który będzie odpowiadać na pytanie, ile podano liczb k-sfenicznych w ciągu liczb naturalnych dodatnich począwszy od indeksu w przedziale [a..b], gdzie a to indeks początkowy przedziału, natomiast b to indeks końcowy (wyrazy ciągu indeksujemy od 1).

Wejście

W pierwszym wierszu jedna liczba naturalna n określająca długość ciągu (nie więcej niż milion).

W drugim wierszu n liczb naturalnych dodatnich nie większych niż milion.

Następnie jedna liczba q określająca liczbę zapytań. Każde zapytanie składa się z trzech liczb całkowitych a, b i k takich, że 1 ≤ a ≤ b ≤ n definiujących przedział [a..b] oraz 1 ≤ k ≤ 20, określająca ilość liczb pierwszych w rozkładzie badanych liczb.

Wyjście

Dla każdego zapytania jedna liczba określająca liczbę liczb sfenicznych o k rozkładzie.

Przykład

Wejście:
7
3 6 8 9 20 13 80
5
1 7 3
1 7 1
2 6 2
5 7 3
1 1 1

Wyjście:
0
2
1
0
1

FR_07_16 - Zawody

 

Zawody

Jasiu i jego robot bierze udział w zawodach. Robot może poruszać się po prostokątnej mapie pól w metryce miasto. Startuje z lewego górnego pola do prawego dolnego i wraca z powrotem do punktu startu. Kiedy idzie na południowy-wschód może poruszać się tylko w prawo lub na dół, a w drodze powrotnej może poruszać się wyłącznie w lewo lub do góry. Robot powinien obrać taką drogę, aby odwiedzić jak najwięcej oznaczonych pól z gwiazdkami, przy czym robot nie może przechodzić przez pola oznaczone znakiem x. Po zbadaniu mapy, Jasiu zdaje sobie sprawę, że zadanie nie jest takie proste i trzeba robota odpowiednio zaprogramować. Dlatego uprzejmie prosi Ciebie o pomoc w napisaniu programu, który pozwoli robotowi optymalnie przejść mapę. Mając do dyspozycji mapę 2D, w której zaznaczone są pola z gwiazdkami oraz pola x, po których robot poruszać się nie może, wyznacz maksymalną liczbę pól z gwiazdkami, do których robot może dotrzeć. Pola z gwiazdkami odwiedzone dwa razy liczone są tylko raz.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę zestawów danych. W pierwszym wierszu każdego zestawu znajdują się dwie liczby całkowite a, b (2 ≤ a, b ≤ 100) oznaczające długość i szerokość mapy. W kolejnych wierszach opisana jest mapa złożona z b wierszy, każdy wiersz po aznaków o następujących oznaczeniach:
. - chodnik, po którym może poruszać się robot
* - pole z gwiazdką 
x - pola, po których robot poruszać się nie może

Należy założyć, że lewe górne pole oraz prawe dolne to pole, w którym nie ma znaku x oraz, że istnieje co najmniej jedna droga łącząca lewe górne pole z polem prawym dolnym.

Wyjście
Na wyjściu, dla każdego przypadku testowego, należy wypisać maksymalną liczbę pól z gwiazdkami, które robot może odwiedzić.

Przykład

Wejście
2
8 6
*.......
....**x.
..**..x*
.*xxx*..
...x*.x*
*.......
5 5
.*...
.xxx.
*.*.*
.xxx.
.*.*.

Wyjście
7
5

FR_07_17 - Bajtogalareta

 

Jak w wielu krajach, również w Bajtocji mieszkańcy wymyślili swój narodowy deser: bajtogalaretę. Są to galaretki zanużone w budyniu. Przysmak jest jednak w fazie testów. Przygotowuje się go w pojemnikach o wymiarach a[dm] x b[dm] x 1 dm. Najpierw do formy wpuszcza się sześcienne galaretki o objętości 1 dm3 każda. Zatrzymują się one w różnych miejscach pojemnika, ale ich odległości od jego dna oraz brzegów wyrażone w decymetrach są zawsze liczbami całkowitymi (specjalna receptura). Następnie od góry zalewa się je budyniem. Ten oczywiście ścieka na dół formy, gdy jednak spotyka na swojej drodze galaretkę, to połowa płynie na lewą stronę, a połowa na prawą. Gdy budyń nie mieści się z jednej strony, to przepływa na drugą. Jako że formy są szybko schładzane, nie działa tu zasada naczyń połączonych. Kucharze pracują jeszcze nad optymalną gęstością bajtogalarety i chcieliby prowadzić statystyki mówiące o tym, ile budyniu zajduje się w każdej kolumnie o szerokości 1 dm. Pomóż im i napisz program, który po prześwietleniu formy odpowie na ich pytanie.

Input

Na początku zostaną podane 4 liczby całkowite: a i b (a,b<=100) oznaczające wymiary formy, w (0<w<=a) mówiąca, na którym decymetrze od lewej strony znajduje się wlew budyniu oraz l oznaczająca ilość budyniu do dyspozycji w dm3.

Następnie do wczytania będzie b wierszy po a znaków "0" lub "1" oznaczających kolejno miejsce puste lub wypełnione galaretą. W każdym przypadku testowym budyń mieści się w pojemniku.

Output

Na wyjściu wypisz a liczb rzeczywistych odpowiadających ilości budyniu w każdej kolumnie pojemnika.

Example

Input:
14 8 6 22
00000000000000
01010110000000
01010100000000
00111101100000
10000101000000
00000111010000
01000001001010
00000001001000


Output:
1 1 3 1 3 1 3 0 2.5 2 0 2 1 1.5

FR_07_18 - Tentaizu

 

Tentaizu

Tentaizu to japońska gra umysłowa, której reguły przypominają trochę reguły popularnego sapera. Tentaizu to diagram 7 × 7, w którym dokładnie 10 spośród 49 pól to ukryte gwiazdy. Na podstawie wskazówek w postaci odkrytych liczb, należy ustalić, w których polach znajdują się gwiazdy. Liczba w polu określa, z iloma polami z gwiazdami sąsiaduje to pole poziomo, pionowo lub skośnie. Żadne pole liczbowe nie zawiera gwiazdy, ale gwiazda może zawierać się w polu, w sąsiedztwie której nie ma pól liczbowych. Jak się zapewne domyślasz, zadaniem Twoim jest napisanie programu, który rozwiąże Tentaizu.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę przypadków testowych. W kolejnych wierszach znajdują się przypadki testowe. Każdy przypadek to początkowe Tentaizu, czyli diagram 7 × 7, na który składa się 7 wierszy po 7 znaków w każdym wierszu. Każe pole diagramu to albo znak kropki, albo liczba z przedziału [0-8]. Pomiędzy przypadkami testowymi znajduje się dodatkowy znak końca linii. 

Wyjście
Na wyjściu wydrukuj rozwiązany diagram Tentaizu w tym samym formacie co diagram wejściowy. Rozwiązany diagram oznacza, że należy zastąpić znakiem gwiazdki dokładnie 10 pól oznaczonych znakiem kropki. Należy założyć, że każdy diagram na wejściu ma dokładnie jedno unikalne rozwiązanie. Między wydrukowanymi diagramami może znajdować się dodatkowy znak końca linii.

Przykład

Wejście
2
.....1.
....22.
.1.....
..231.1
...1...
......3
..3..2.

1....0.
.1.....
1..3...
..23.2.
..3....
.3....2
1.1..2.

Wyjście
....*1.
....22.
.1*.*..
..231.1
..*1..*
.*...*3
.*3*.2*

1....0.
*1.*...
1..3*..
..23*2.
.*3*...
*3*..*2
1.1..2*

FR_07_19 - Sciezka

 

Jasio po godzinach spędzonych z matematyką musi czasem od niej odpocząć. Lubi wtedy grać w gry MMORPG. Królowa nauk jest jednak obecna i tutaj. Jasio w swojej grze ma do wykonana kilka zadań (questów). Aby wykonać każdy z nich, trzeba odwiedzić kilka miejsc. Miejsca są ze sobą połączone, ale żeby dostać się z jednego do drugiego, trzeba zapłacić określoną kwotę. Można jednak wyznaczyć optymalną trasę między nimi, wykonując kilka zadań w jednym czasie. Pomóż Jasiowi i oblicz, jaką najmniejszą kwotę musi przygotować, by wykonać wszstkie zadania.

Input

Na początku zostaną podane dwie liczby: m(m<100) oznaczająca ilość wszystkich miejsc oraz s(s<300) oznaczająca ilość dostępnych ścieżek między nimi. W kolejnych m liniach na wczytanie będą czekać nazwy miejsc (nie występują w nich spacje i nazwa jest krótsza niż 35 znaków). Potem podanych będzie s linii zawierających informacje o  ścieżkach: jakie miejsca łączą oraz jaki jest koszt podróży. W kolejnej linii znajduje się miejsce startowe. Na końcu wejścia do wczytania będzie od 1 do 3 linii. Każda z nich to zadanie złożone z nieokreśclonej liczby miejsc do odwiedzenia, jednak łączna ich ilość nie przekracza 50.

Output

Na wyściu ma znaleźć się jedna liczba oznaczająca kwotę potrzebną do wykonania wszystkich zadań.

Example

Input:
10 31
Town_of_Schuttgart
Town_of_Goddard
Rune_Township
Town_of_Aden
Town_of_Oren
Town_of_Giran
Town_of_Dion
Town_of_Gludio
Gludin_Village
Heine
Town_of_Schuttgart Town_of_Goddard 10000
Town_of_Goddard Rune_Township 10000
Town_of_Goddard Town_of_Aden 8100
Town_of_Goddard Town_of_Schuttgart 10000
Rune_Township Town_of_Goddard 10000
Rune_Township Town_of_Oren 10000
Rune_Township Town_of_Aden 37000
Town_of_Aden Town_of_Goddard 8100
Town_of_Aden Rune_Township 37000
Town_of_Aden Town_of_Oren 6900
Town_of_Aden Hunters_Village 5900
Town_of_Aden Town_of_Oren 6900
Town_of_Aden Town_of_Giran 13000
Town_of_Oren Town_of_Aden 6900
Town_of_Oren Rune_Township 10000
Town_of_Oren Hunters_Village 4100
Town_of_Oren Town_of_Giran 9400
Hunters_Village Town_of_Oren 4100
Hunters_Village Town_of_Aden 5900
Town_of_Giran Town_of_Aden 13000
Town_of_Giran Town_of_Oren 9400
Town_of_Giran Town_of_Gludio 29000
Town_of_Giran Town_of_Dion 6800
Town_of_Giran Heine 7600
Heine Town_of_Giran 7600
Heine Town_of_Dion 12000
Town_of_Dion Heine 12000
Town_of_Dion Town_of_Giran 6800
Town_of_Dion Town_of_Gludio 3400
Town_of_Gludio Gludin_Village 7300
Gludin_Village Town_of_Gludio 7300
Town_of_Goddard
Town_of_Gludio Town_of_Oren Town_of_Schuttgart
Heine Town_of_Oren Gludin_Village Gludin_Village
Rune_Township Town_of_Oren

Output:

100400

 

FR_07_20 - Lider II

 

W Dwójkolandii przyszedł czas na długo wyczekiwane wybory. Okręgi wyborcze wystawiły swoich kandydatów, a wyborcy zapoznali się z ich planami wyborczymi. Dziś jest dzień wyborów, a ty zostałeś powołany na wolontariat polegający na zliczaniu głosów i określeniu, czy w danym okręgu wyborczym jakiś kandydat osiągnął więcej niż 50% głosów. System wyborczy w Dwójkolandii działa następująco. Wyborcy należący do danego okręgu wyborczego są zapisani na spójnej liście, jeden za drugim, itd. Wszystkie listy połączone są w jedną wielką listę. Dodatkowo każdy wyborca ma prawo zmienić swój wybór i zaznaczyć innego kandydata - taki system :). Ty jednak jesteś bardzo sprytną osobą i pojąłeś trudną sztukę programowania. Napisz program, który znacznie ułatwi ci pracę na wolontariacie, wyznaczający lidera w przedziale liczb. Wykonujemy dwie operacje. Pierwsza, to zmiana wyboru kandydata na inny (zmiana decyzji wyborcy), druga to sprawdzenie, czy w okręgu zaczynającym się od wyborcy na pozycji a a kończącym się na wyborcy na pozycji b został wybrany kandydat do rządzenia Dwójkolandią - tzn. liczba oddanych głosów na tę osobę jest większa niż 50%.

Wejście

W pierwszym wierszu jedna liczba n określająca liczbę wyborców (nie więcej niż 10⁶).

W drugim wierszu n liczb naturalnych określających głosy wyborców. Każdy kandydat jest reprezentowany przez liczbę mieszczącą się w przedziale [0..10⁹]. Jeden kandydat może być wybierany w kilku okręgach (taki system :)).

W trzecim wierszu jedna liczba q określająca liczbę zapytań (nie więcej niż 10⁶).

Specyfikacja każdego zapytania:

najpierw jeden znak i lub q, następnie dwie liczby całkowite. Jeśli pojawi się i, zostaną podane dwie liczby całkowite x i y, oznaczające, że należy podmienić decyzję wyborcy z pozycji x w ciągu na y, natomiast, gdy pojawi się znak q, to pojawią się dwie liczby a i b, definiujące przedział [a...b], w którym należy określić, czy występuje lider w tym przedziale (1 ≤ x ≤ n, 0 ≤ y ≤ 10⁹, 1 ≤ a ≤ b ≤ n).

Wyjście

Dla każdego zapytania, w którym wystąpiła litera q należy wypisać lidera zbioru w przedziale [a..b], lub napis brak, gdy lider nie występuje.

Przykład

Wejście:
6
2 2 3 2 7 8
5
q 1 4
q 1 1
i 3 7
q 3 5
q 3 6


Wyjście:
2
2
7
brak